前言
有时候我们在阅读论文时会发现,里面的图不仅美观,而且能够一步步展示数据的特征与规律。但是对于很多想自己动手画图的小伙伴来说,可能会觉得无从下手。其实,你只需要掌握一些简单的 Python 基础和数据处理技巧,就能快速复刻出类似论文中的精彩图像!
这是我们今天主要复刻的图像:
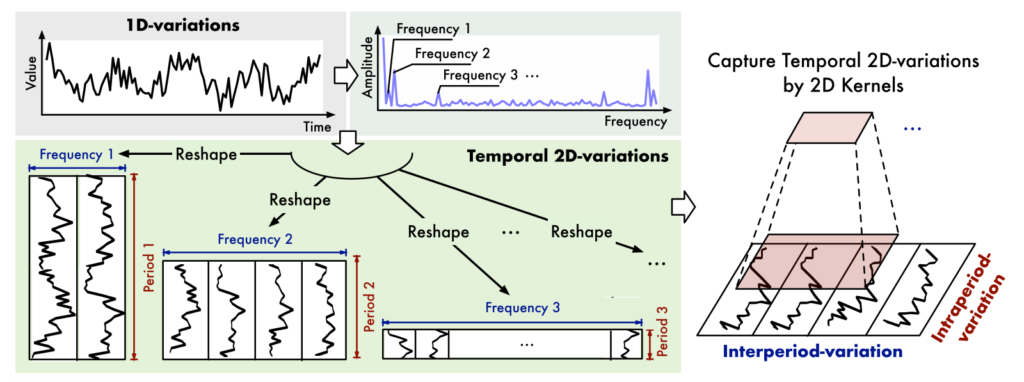
这篇论文是:TIMESNET: TEMPORAL 2D-VARIATION MODELING FOR GENERAL TIME SERIES ANALYSIS
这篇博客主要包含了以下内容:
- 合成一维时间序列:随机游走 + 周期信号 + 噪声
- 去趋势处理(detrend)并绘制“时域图”
- 对信号进行快速傅里叶变换(FFT),并绘制“频域图”
- 识别主要频率与周期
- 按不同主要周期对时序信号进行重塑(reshape),并依次可视化
- 最后,用 PPT 将多张图拼接成示意图,说明如何从 1D 信号到 2D 的时频变化,再到 2D 卷积核捕捉特征的过程
不必害怕代码——所有代码都是一步步给出的,而且每一部分都会有详细解释。如果你是小白,也能在这篇博客里学到不少干货噢!
一维时间序列的合成与可视化
下面是第一段代码,主要作用是生成一个随机时间序列,并叠加几个不同频率与不同振幅的正弦波,最后再加上一点噪声。最后,我们用 detrend 来去掉整体趋势(即 DC 分量),并画出时域图和频域图。
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
from scipy.signal import detrend
# 设置中文字体为 SimHei(黑体),以便在图表中正常显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 避免负号 '-' 显示为方块
# 设置随机种子以确保结果可重复
np.random.seed(42)
# 生成时间轴
time_steps = np.arange(0, 100, 0.1) # 时间范围从 0 到 100,步长为 0.1 秒
T = 0.1 # 采样间隔(Sampling Interval)
N = len(time_steps) # 数据点总数
# Step 1: 随机游走生成
# np.random.randn(N) 会生成 N 个服从标准正态分布的随机数
# np.cumsum(...) 会对随机数做累加,模拟“随机游走”过程
random_walk = np.cumsum(1 * np.random.randn(N))
# Step 2: 生成几个正弦波周期信号,增加振幅和频率范围
# frequencies 列表中存放了四个主要频率
# amplitudes 列表中存放了对应的振幅大小
# phases 存放每个正弦波的初始相位
frequencies = [0.1, 0.3, 0.7, 1.8] # 四个主要频率 (Hz)
amplitudes = [25, 40, 20, 15] # 对应的增强振幅
phases = [0, np.pi / 4, np.pi / 2, np.pi / 3] # 每个正弦波的初始相位
# 将四个正弦波循环累加得到一个综合的周期信号
periodic_signal = sum(
amplitude * np.sin(2 * np.pi * freq * time_steps + phase)
for amplitude, freq, phase in zip(amplitudes, frequencies, phases)
)
# Step 3: 合成信号(随机游走 + 周期信号 + 噪声)
noise_amplitude = 50 # 设定噪声的整体幅度
noise = noise_amplitude * np.random.randn(N) # 生成高斯白噪声
final_signal = random_walk + periodic_signal + noise # 三部分叠加
# Step 3.1: 去除信号的整体趋势(DC 分量)
# detrend 函数会将信号的线性趋势去掉,同时也能减少均值偏移
final_signal = detrend(final_signal)
# Step 4: 绘制时间序列(时域图)
plt.figure(figsize=(20, 4), facecolor='white') # 创建画布,设置背景为白色
plt.plot(time_steps, final_signal, color='green', label='最终信号')
plt.xlabel('时间 (s)')
plt.ylabel('信号值')
plt.title('增强振幅的一维时间序列 (去趋势后)')
plt.grid(False) # 不显示网格
plt.xticks([]) # 不显示 x 轴刻度
plt.yticks([]) # 不显示 y 轴刻度
plt.legend()
plt.show()
# Step 5: 傅里叶变换(FFT)
# fft(final_signal) 得到复数形式的频谱
# fftfreq(N, T) 生成与 FFT 对应的频率轴
yf = fft(final_signal)
xf = fftfreq(N, T)[:N // 2] # 只取正频率部分,[:N//2] 代表前半段
amplitude_spectrum = 2.0 / N * np.abs(yf[:N // 2]) # 计算幅度谱
# Step 6: 绘制频谱图(频域图)
plt.figure(figsize=(15, 5), facecolor='white')
plt.plot(xf, amplitude_spectrum, color='blue', label='振幅谱')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅度')
plt.title('傅里叶变换后的频谱图(去趋势后)')
plt.grid(False)
max_freq = 3 # 只关心 0 ~ 3 Hz 范围
plt.xlim(0, max_freq)
plt.xticks([]) # 不显示 x 轴刻度
plt.yticks([]) # 不显示 y 轴刻度
plt.ylim(-10, 60)
# 下面这段标注主要频率的代码只做简单演示,并未实际绘制在图上
for freq, amp in zip(frequencies, amplitudes):
idx = np.argmin(np.abs(xf - freq)) # 找到与 freq 最接近的频率索引
actual_freq = xf[idx]
actual_amp = amplitude_spectrum[idx]
# 如果需要在图上做标记,可以用 plt.annotate 或 plt.text
plt.legend()
plt.show()
结果解读:
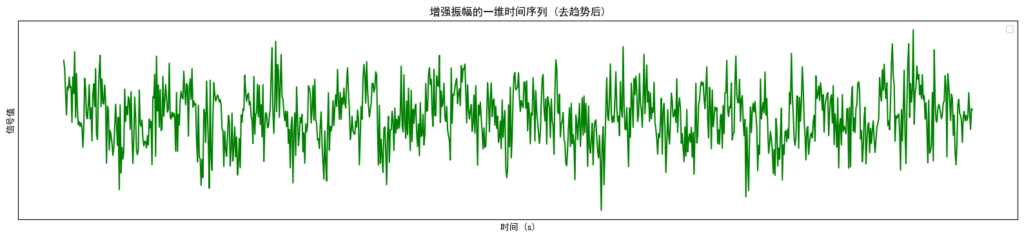
时域图:我们先看第一张输出的绿色曲线——这就是在随机游走基础上叠加了四个正弦波,以及一定量高斯噪声后得到的去趋势后信号。去趋势的作用是为了去掉累加造成的“整体抬升”或“整体降低”。
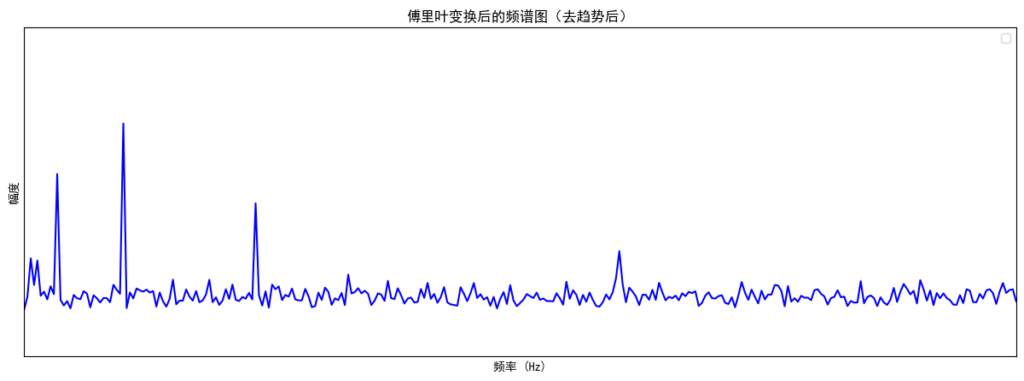
频域图:第二张蓝色频谱图可以看到几个比较明显的“尖峰”,这些就是我们人为叠加的主要频率(0.1, 0.3, 0.7, 1.8 Hz 等)带来的谱峰。
看完这两张图,你就能理解到,一个人造的时间序列如何从时域和频域两个维度表现出不同的特性。
周期拆分与可视化(第一种主要周期)
当我们通过频谱图识别到主要频率后,就能进一步计算得到其主要周期(period = 1 / frequency)。接下来,我们就想把整段时间序列,按照这个主要周期拆分(reshape)成多个小片段,看看每一个周期内的波形究竟长什么样子。
接下来就是第二段示例代码。
# Step 1: 根据频谱图识别主要频率
# 对 amplitude_spectrum 从小到大进行排序,然后选取最大的 3 个值所对应的频率
dominant_frequencies = xf[np.argsort(amplitude_spectrum)[-3:]]
dominant_frequencies = np.sort(dominant_frequencies) # 从小到大排序,便于阅读
print("主要频率:", dominant_frequencies)
# 计算相应的主要周期
# 周期 = 1 / 频率
dominant_periods = 1 / dominant_frequencies
print("主要周期(Period):", dominant_periods)
# Step 1: 确定主要周期(这里使用 dominant_periods[0],即第一个主要周期)
period = dominant_periods[0]
period_steps = int(period / T) # 计算一个周期在采样点层面的大小
# Step 2: 重塑时间序列
# num_periods 表示整个信号在这个周期下最多可以分多少个完整周期
num_periods = len(final_signal) // period_steps
# 只取前 (num_periods * period_steps) 个点,避免最后不完整的周期
reshaped_series = final_signal[:num_periods * period_steps].reshape((num_periods, period_steps))
# Step 3: 分开绘制每个周期的折线图
# 这里为了示例,先只画前两个周期
plt.figure(figsize=(15, num_periods * 3))
plt.rcParams['axes.facecolor'] = 'white' # 设置图表背景为白色
for i in range(2): # range(2) 表示画出前两个周期
plt.subplot(num_periods, 1, i + 1) # 创建子图 (按行排列)
plt.plot(range(period_steps), reshaped_series[i], color='red', label=f'周期 {i+1}')
plt.xlabel('周期内时间步数')
plt.ylabel('信号值')
plt.title(f'第 {i+1} 个周期')
plt.legend(loc='upper right')
# 限制 x 轴的范围为 0 到 100,这里是可根据需要调整的
plt.xlim(0, 100)
# 自动调整子图之间的间距,防止重叠
plt.tight_layout()
plt.show()结果解读:
上面的代码先找到了频谱中“幅值最大的三个频率”,并将它们分别反算出三个主要周期。
接着,我们使用其中的第一个主要周期(dominant_periods[0]),来对信号进行“整除裁剪 + reshape”的操作:
period_steps = int(period / T):把一个周期对应的采样点数算出来;
reshaped_series 就是一个二维数组了,每一行代表一个周期。
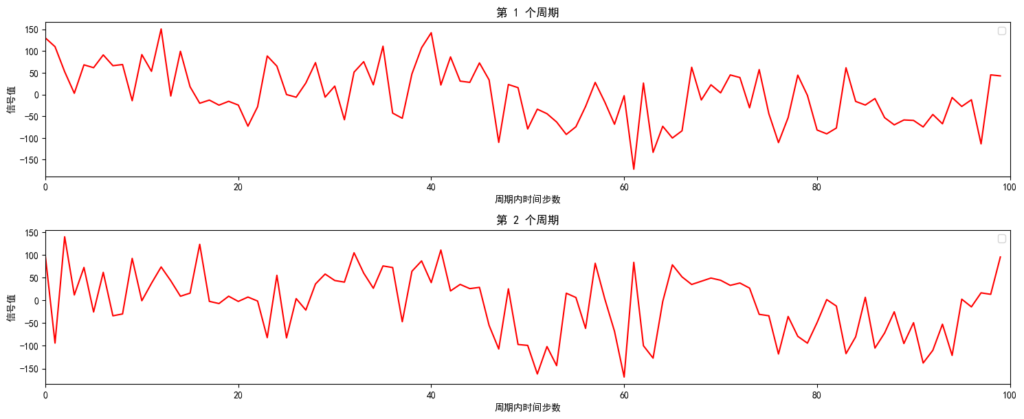
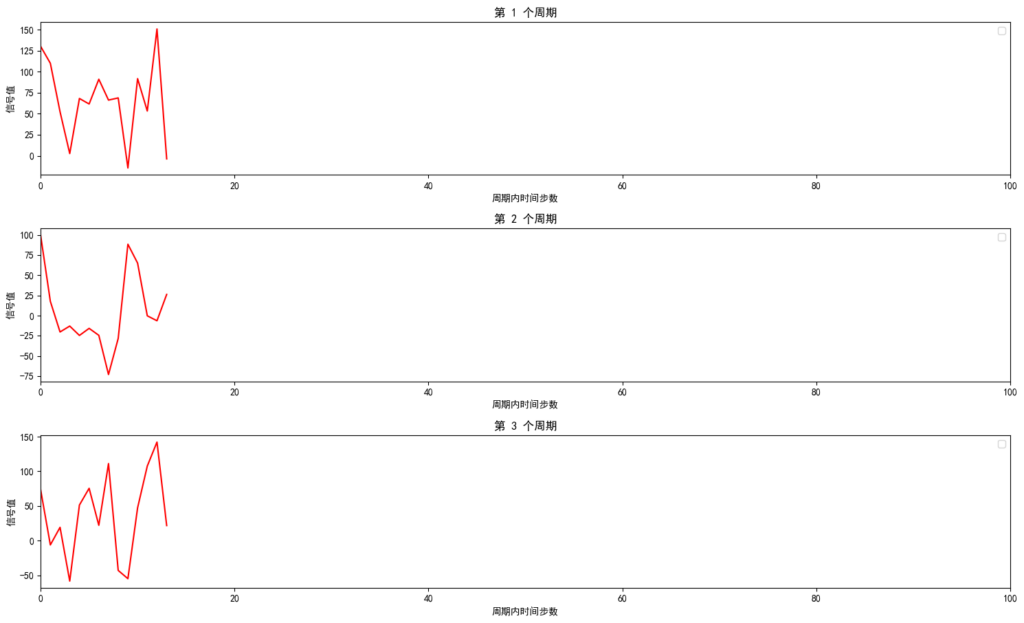
最后,我们依次把每个周期的波形画出来(这里为了展示,只画了前两个周期)。
如果你看输出的图,会发现第一张图和第二张图各显示了一个周期的数据,随着周期不同,波形也略有差异。
周期拆分与可视化(第二种主要周期)
第三段代码与上一段基本相似,只是换了主要周期。这样我们就能对同一个信号,用不同的周期来进行分段观察。
# Step 1: 确定主要周期(使用 dominant_periods[1],即第二大主要频率对应的周期)
period = dominant_periods[1]
period_steps = int(period / T) # 计算一个周期对应的采样点数
# Step 2: 重塑时间序列(与前面一致的思路)
num_periods = len(final_signal) // period_steps
reshaped_series = final_signal[:num_periods * period_steps].reshape((num_periods, period_steps))
# Step 3: 分开绘制每个周期的折线图
# 这里我们绘制前四个周期,可根据需求调整
plt.figure(figsize=(15, num_periods * 3))
plt.rcParams['axes.facecolor'] = 'white'
for i in range(4): # 假设想看前四个周期
plt.subplot(num_periods, 1, i + 1)
plt.plot(range(period_steps), reshaped_series[i], color='red', label=f'周期 {i+1}')
plt.xlabel('周期内时间步数')
plt.ylabel('信号值')
plt.title(f'第 {i+1} 个周期')
plt.legend(loc='upper right')
# 限制 x 轴范围为 0 到 100,仅作演示
plt.xlim(0, 100)
plt.tight_layout()
plt.show()结果解读:
这次用的是 dominant_periods[1],也就是排序后第二大的主要频率对应的周期。
画出来的周期波形会和前一个周期拆分不一样,因为这里的“一个周期”在时间上更长或更短。
如果输出的周期数还比较多,可以用循环再多画几张图。

周期拆分与可视化(第三种主要周期)
同理,第四段代码用的就是 dominant_periods[2]。
如果想画更多周期,可以再修改循环里 range(3) 这个值。
# Step 1: 确定主要周期(使用 dominant_periods[1],即第二大主要频率对应的周期)
period = dominant_periods[1]
period_steps = int(period / T) # 计算一个周期对应的采样点数
# Step 2: 重塑时间序列(与前面一致的思路)
num_periods = len(final_signal) // period_steps
reshaped_series = final_signal[:num_periods * period_steps].reshape((num_periods, period_steps))
# Step 3: 分开绘制每个周期的折线图
# 这里我们绘制前四个周期,可根据需求调整
plt.figure(figsize=(15, num_periods * 3))
plt.rcParams['axes.facecolor'] = 'white'
for i in range(4): # 假设想看前四个周期
plt.subplot(num_periods, 1, i + 1)
plt.plot(range(period_steps), reshaped_series[i], color='red', label=f'周期 {i+1}')
plt.xlabel('周期内时间步数')
plt.ylabel('信号值')
plt.title(f'第 {i+1} 个周期')
plt.legend(loc='upper right')
# 限制 x 轴范围为 0 到 100,仅作演示
plt.xlim(0, 100)
plt.tight_layout()
plt.show()结果解读:
经过这样的对比,我们就可以知道:针对同一个信号,如果从不同的“主要周期”去进行分段与重塑,对应看到的周期内波形是非常不一样的。
这在实际科研中有时很有价值:比如我们想聚焦哪个频率,就可以用它对应的周期进行折叠分析。
最后一张示意图:从一维到二维再到卷积
最后一张图(或示意图)往往是为了让读者快速理解你做了什么操作。论文里经常会用一些“多图拼接”的方式呈现。实际上,这种图未必一定是编程自动生成的,有时手动用 PPT 拼接会更直观、也更美观!
- 你可以将“时域图”和“频域图”截下放在左侧,表示这是你的原始数据(1D 时间序列 + 1D 频谱)。
- 再把“多个周期重塑之后的折线图”按行或按列拼接在中间,表示你获得了一个“2D 矩阵”(行对应周期,列对应频率或时间步)。
- 最后在右边示意一下:如果使用 2D 卷积的方式,就能同时捕获周期之间的差异(inter-period variation)和周期内部每个点的差异(intra-period variation)。
比如下图所示(这里是一个自制的 PPT 图):
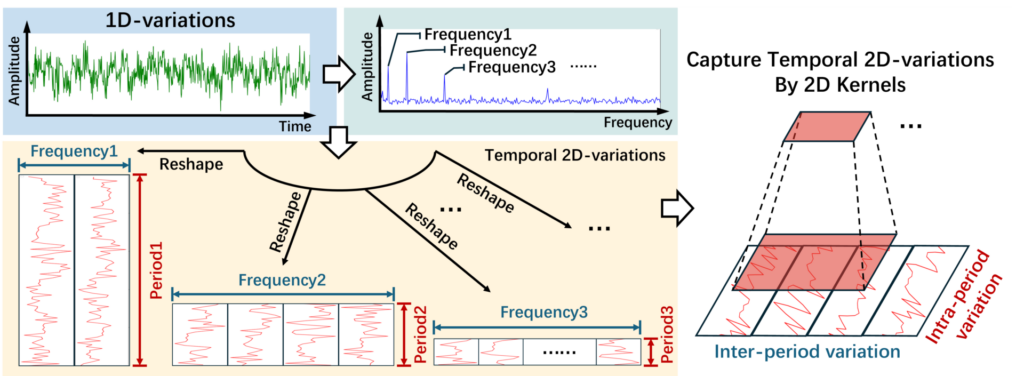
和原图对比,你觉得哪张更好看呢?

重点:在论文中,示意图可以帮助你向读者快速阐述自己的思路,而不需要他们一行行地阅读你的代码。对于新人科研人员来说,画好示意图能让审稿人对你的方法一目了然哦!
小结
通过上述步骤,你已经学会了如何:
- 合成一个带随机游走、多个正弦波、噪声的时间序列
- 去趋势、绘制时域图以及快速傅里叶变换后绘制频域图
- 用识别到的主要周期分段重塑该信号,并分别可视化每个周期
- 用 PPT(或其他工具)拼成一张“思路示意图”,从 1D 到 2D 再到卷积特征提取的效果
当你掌握了这些基础操作,以后读论文时,看到作者在做各种时域分析和频域分析的时候,就可以轻松地自己“复刻”他们的图表了。更重要的是,你也能用同样的思路去分析自己的数据,找到数据背后的周期特征与频域规律。
下一步:你可以尝试改变一些参数,比如增加/减少叠加的正弦波数量,更改噪声幅度,或者更改采样步长 T 与总采样时长,看看最后时域图和频域图会发生什么变化。通过不断地试验,你会对时频分析和周期性信号有更加深刻的体会!
参考和延伸阅读
最后,恭喜你已经完成了一次“论文图表复刻小实践”!学会之后,你就能在自己的科研或项目中更自如地呈现数据特征和规律。
如果你觉得这篇文章对你有帮助,欢迎在评论区留下你的问题或想法,一起交流探讨~